电子设备可靠性的基本概念
2.电子设备可靠性的数学描述在可靠性的定量测定方面,使用最广泛的是统计方法,概率论和数学统计学是研究可靠性问题的主要工具。概率论能确定影响可靠性的可变随机变数的大数与可靠性数量特征之间的相互关系。因此,可靠性理论的许多概念与概率论中所用的概念有关。概率论能研究普遍现象,多次试验时重复的现象称为普遍现象。如果在多次试验时,每一次试验必然发生某一事件,则该事件称为必然事件。如果某一事件明知不会发生,则称为不可能事件。在每一次单独试验中不可能预言的事件称为随机事件。除随机事件之外,概率论还研究随机变数及随机过程(随机函数)。由于试验的结果可取某一值的变数,如产品尺寸与其额定值的误差,焊点失效前的工作时间等,因而称为随机变数。与某些非随机变数的不同值相符的随机变数的集合,如焊接温度的起伏等,称为随机过程或随机函数。准确地预言随机变数、随机过程及随机事件是不可能的。但是,如果研究的不是每一个随机事件、随机变数或随机过程,而是它们的集合,则可用数学方法来说明其特征。假设做N次试验时,某一事件A出现K次,这时,K/N的比例称为随机事件A的频率并以W(A)表示,即W(A)=K/N当试验次数增多后,事件A出现的频率就显得较稳定,即在相同条件下进行多次试验时,事件的频率近似于P,即P(A)=K/N (1)P(A)称为事件A的概率并写成P=P(A) (2)从式(1)和式(2)可看出,做N次试验时,事件A约发生NP次,而不发生N(1-P)次。显然,随机事件的概率在数量上符合条件0≤P≤1如果A是不可能事件,则P=0;如果A是必然事件,则P=1。对于随机事件,研究计算概率的基本法则是:(1)如果事件A1,A2,…,An是不相容的,则P( A1+A2+…+An )=P(A1)+P(A2)+…+P(An)(2)对立事件?的概率可表示为P(?)=1-P(A)(3)几个独立事件联合发生的概率等于这些事件的概率之积,即
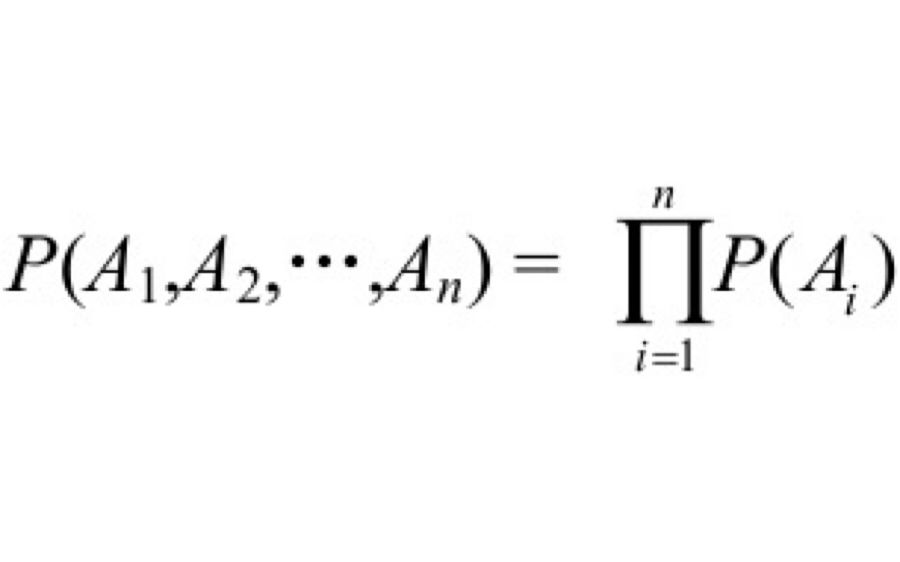
(4)如果事件A和B不是对立和独立的,即如果A和B是任何随机事件,则P(A+B)=P(A)+P(B)- P(AB);P(AB)=P(A)PA(B)式中 PA(B)——在发生事件A的条件下,事件B出现的概率。随机变数往往是离散的或连续的,它可用概率分布函数来说明。设ζ为一随机变数,取小于某个x的值,有P(ζ<x)=F(x)这一事件的概率称为概率分布的积分函数或随机变量的概率分布定律。如果其导数存在,则该函数的导数为F(x)=F'(x)称为随机变量的概率分布函数或密度。随机变量与概率分布函数一样,可用下列数量分布特征来说明。(1)随机变量ζ的平均值或数学期望:
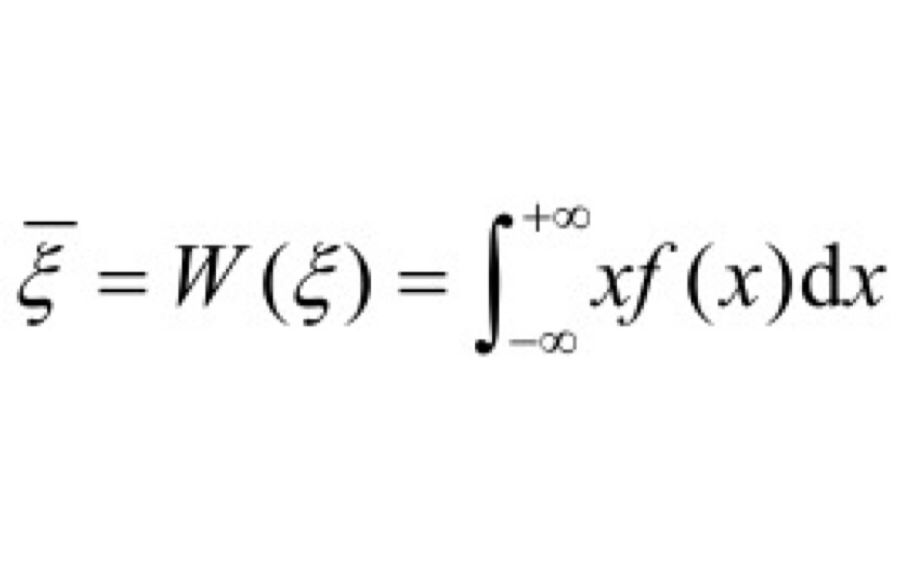
(2)随机变量绝对值的平均算术值或数学期望:
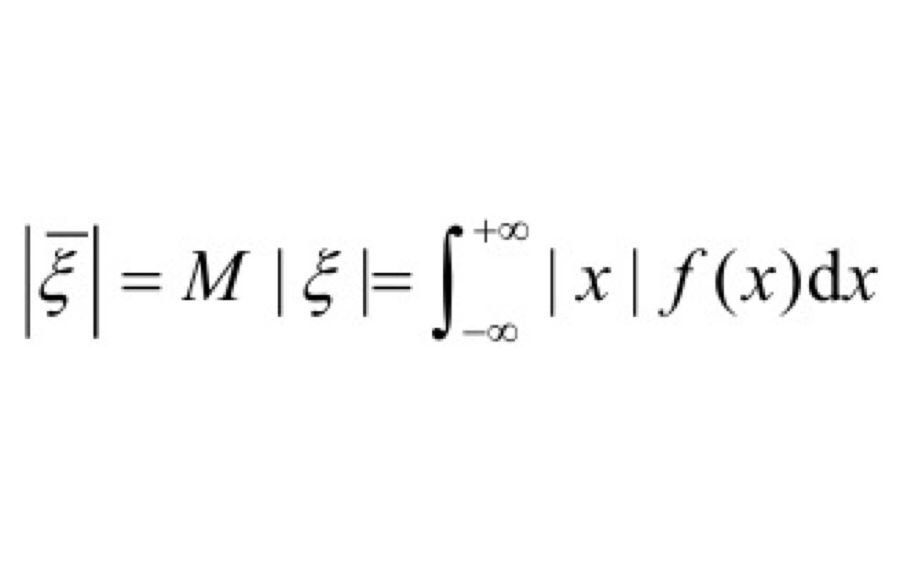
(3)随机变量的随机(平均)值b,即其值在区间(-b<ζ<b)内,存在于区间内的概率等于0.5。b值由下式计算。
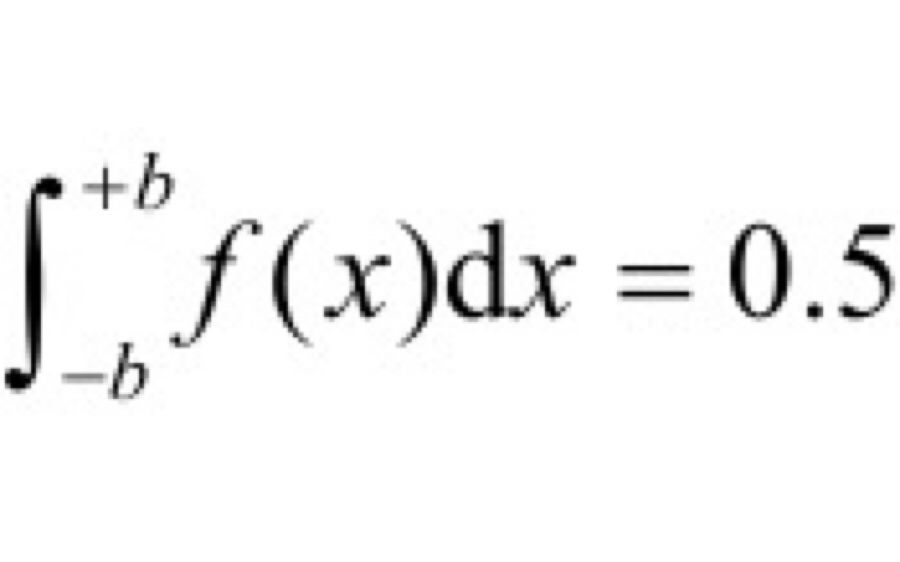
(4)随机变量ζ的平方平均值:
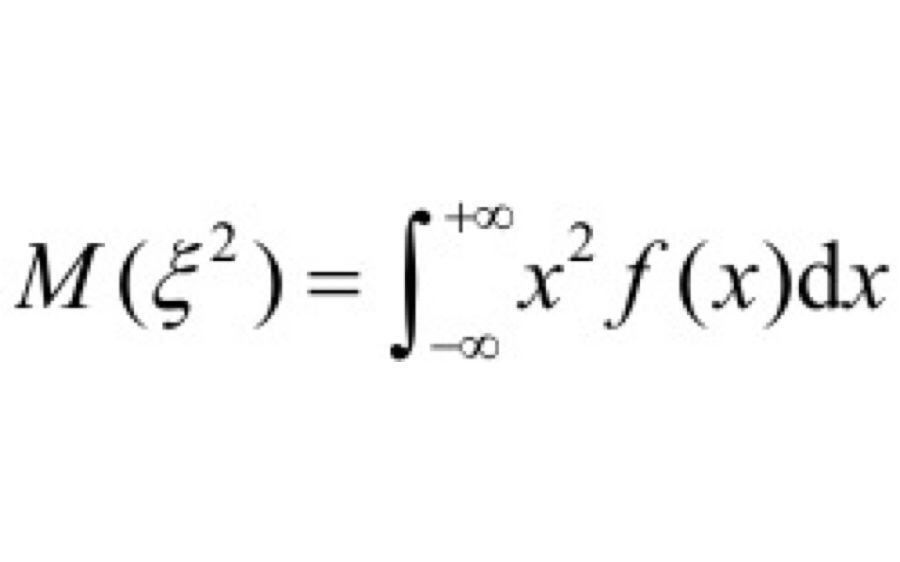
(5)随机变量的方差:
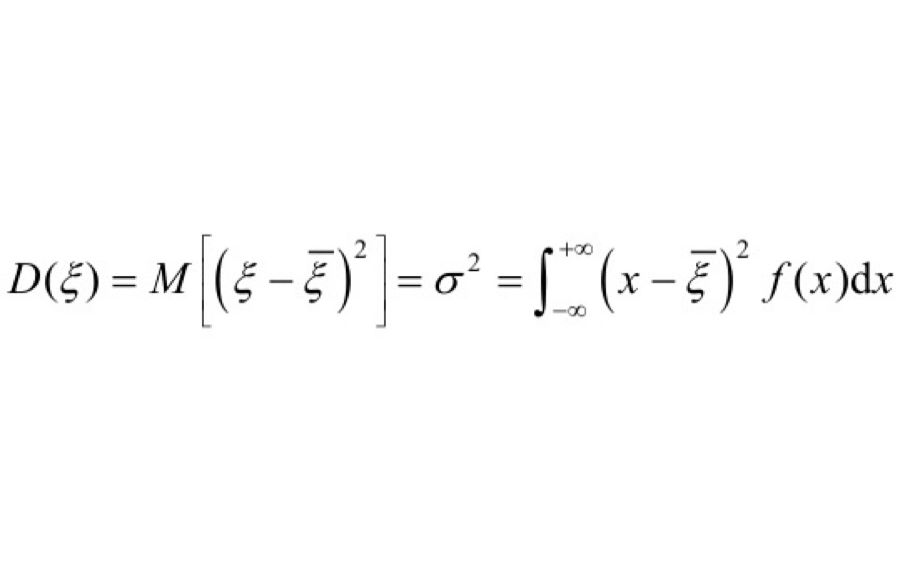

图片新闻
最新活动更多
-
6月13日立即参评>> 【评选】维科杯·OFweek2025中国工业自动化及数字化行业年度评选
-
即日-6.16立即报名>> 【在线会议】olution Talks |Computex 2025关键趋势深读
-
7月22-29日立即报名>> 【线下论坛】第三届安富利汽车生态圈峰会
-
7.30-8.1火热报名中>> 全数会2025(第六届)机器人及智能工厂展
-
7月30-31日报名参会>>> 全数会2025中国激光产业高质量发展峰会
-
即日-2025.8.1立即下载>> 《2024智能制造产业高端化、智能化、绿色化发展蓝皮书》
推荐专题
- 1 数智破局·生态共生:重构全球制造新引擎 2025 WOD制造业数字化博览会即将在沪盛大启幕
- 2 智造赋能,生态共融:大联大携手产业伙伴,共绘新质工业宏伟蓝图
- 3 谁将成为行业榜样?维科杯·OFweek2025中国工业自动化及数字化行业年度评选等您来参与!
- 4 【重磅来袭】6月17日上海见!全球智造巨头聚首,60余场前沿论坛,制造业数字化盛会邀您共启数智破局之旅!
- 5 安森美正式参评“维科杯·OFweek 2025中国工业自动化与数字化行业优秀产品奖”
- 6 当数智工业邂逅大湾区,看PHIIDF2025如何破界,链动全球!
- 7 抢先解锁!全数会2025机器人及智能工厂展览会核心亮点速递
- 8 iEi威强电邀您共襄AIAE Expo 2025北京国际工业自动化盛会,探索智能工业新边界!
- 9 欧姆龙正式参评“维科杯·OFweek 2025中国工业自动化与数字化行业优秀产品奖”
- 10 世界计量日盛会启幕,聚焦测量体系变革:质量、效率与动力







 分享
分享















发表评论
请输入评论内容...
请输入评论/评论长度6~500个字
暂无评论
暂无评论